제 10장 봉형 인식 - 4
극치 분석
극치란 상승기에서 하락기로 바뀌는 순간, 또는 하락기에서 상승기로 바뀌는 순간 즉, 일정 기간 내에서 주가가 가장 높았거나 가장 낮았던 시점에서의 주가를 말한다. 극치 분석(極値 分析)이란 극치에서의 일봉 형태를 분석하는 것을 말한다.
단일봉과 이련봉(二連棒)에 대하여 조사하였다.
a. 단일봉에 대한 극치 분석
◎ 극소 분석
일군(一群)을 형성하고 있는 상위 봉형태는 일자선, 대음봉, 중음봉, 소음봉 등이다.
이들은 앞에서 살펴 보았듯이 상승기나 하락기에서 가장 잘 나타나는 형태이다. 이군(二群)을 형성하고 있는 봉 형태는 윗 수염 달린 장대수염형 들이다. 이들은 상승기나 하락기에서 자주 나타나지 않는 형이었다. 때문에 일군(一群)보다는 이군(二群)의 것들이 발생빈도 면에서는 상대적 차별성을 더 갖는다 하겠다. 제 3장의 동일성원칙(同一性 原則)에서 밝혔듯이 봉형은 상대적 차별성을 가질 때, 봉형의 고유성을 획득한다. 이렇게 볼 때, 극소 상태 즉 추세가 하락기에서 상승기로 바뀌는 순간에 장대 수염형을 특별히 주목할 필요가 있다고 하겠다.
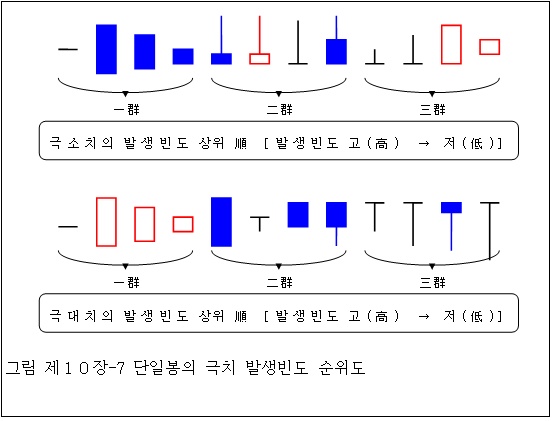
◎ 극대 분석
일군(一群), 이군(二群)을 형성하고 있는 상위 봉 형태는 일자선, 대양봉, 중양봉, 소양봉, 대음봉, 중음봉 등이다.
이들중 일자선과 이군(二群)의 것은 앞에서 살펴 보았듯이 상승기나 하락기에서 가장 잘 나타나는 형태이다. 삼군(三群)을 형성하고 있는 봉 형태는 아랫 수염 달린 장대수염형(長大鬚髥型) 들이다. 이들은 상승기나 하락기에서 자주 나타나지 않는 형이었다. 때문에 일군(一群), 이군(二群)보다는 삼군(三群)의 것들이 발생빈도 면에서는 상대적 차별성을 더 갖는다 하겠다.
극소 분석처럼 극대 상태 즉 추세가 상승기에서 하락기로 바뀔 경우에서도 장대형 수염은 가장 눈여겨 보아야 할 봉형임을 알 수 있다.
◎ 종합
극소 상태에는 주로 윗수염 장대형이, 극대 상태에서는 아랫 수염 장대형이 차별적 특징을 갖고 있다고 분석되었다.
이렇듯 장대형 수염은 추세 변화의 순간에 자주 나타난다. 이는 우리가 여태 알아 보았던 수염 이론에 부합되는 결과라 하겠다.
b. 이련봉에 대한 극치 분석
음양, 양음, 음음, 양양 일련의 2봉 결합 형태에 대해 단일봉과 같은 분석을 행하였다. 조합에 따라 총 4860종의 봉형으로 구분하여 조사하였다. ( [그림 제10장-3]참조 )
◎ 극소 분석
소음봉+소음봉의 제6형, 소음봉+소음봉의 제1형, 소음봉+소음봉의 제14형은 앞의 이련봉 분석에서 살펴 보았듯이 자주 나타나는 봉형이다. 이들 형을 제외하면 (양)포옹선, (양)장대별이 차별적 특징을 갖고 있음을 확인할 수 있다.
이들은 상승 반전형이므로 이론과 부합됨을 알 수 있다.
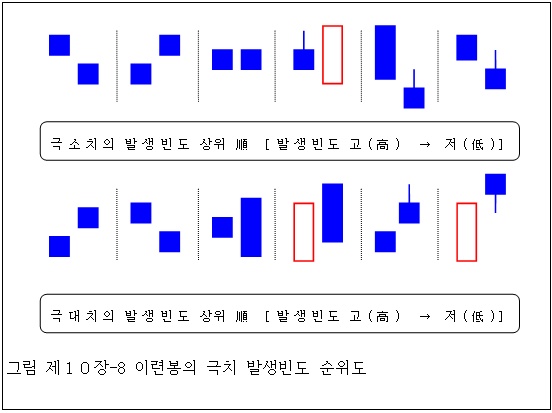
◎ 극대 분석
극소 분석과 같이 자주 나타나는 소음봉+소음봉의 제1형, 소음봉+소음봉의 제6형을 제외하면, 차별적 특징을 갖고 있는 봉형으로는 (음음)포옹선, 피선, (음)장대별을 들 수 있다.
이들은 하락 반전형이므로 역시 이론과 부합되는 결과라 하겠다.
◎ 종합
이련봉 분석에서도 역시 극소에서는 상승 반전형이, 극대에서는 하락 반전형의 출현 빈도가 많다는 것을 실증할 수 있었다.
특히 바닥권에서는 (양)포옹선이, 천정권에서는 피선이 가장 특징적인 반전 신호로 기능한다. 또한 장대별, 즉 장대봉 이후 갭을 만들며 별형이 나타날 때도 반전 가능성이 많다는 것을 다시 한번 확인할 수 있었다.
'주식 > 봉도표' 카테고리의 다른 글
| 제 10장 봉형 인식 - 7 (0) | 2008.04.01 |
|---|---|
| 제 10장 봉형 인식 - 6 (0) | 2008.03.31 |
| 제 10장 봉형 인식 - 5 (0) | 2008.03.29 |
| 제 10장 봉형 인식 - 3 (0) | 2008.03.27 |
| 제 10장 봉형 인식 - 2 (0) | 2008.03.26 |
| 제 10장 봉형 인식 - 1 (0) | 2008.03.25 |





